Appearance
Solar-like
作者:蔡英杰 主分类:pulsation
历史背景
20世纪60年代初Leighton等人首先发现太阳表面任何一点都存在周期大约为5min的上下振动现象,气体平均速度约为0.5~1km/s,并称之为太阳5分钟振动[1]。当时对这种振动的性质尚不清楚。直到1970年,Ulrich等人提出太阳5分钟振动是光球下面不同模式共振声波在太阳表面的叠加[2]。随后Deubner对太阳5分钟振动的观测结果证实了这一预言[3]。从此太阳振动的观测和研究迅速发展,形成了太阳物理中一个新的分支——日震学。
我们使用一词来指代与太阳具有相同振动机制的恒星。虽然叫做,但是其中一些恒星与太阳有着非常大的差异[4]。当在太阳上首次发现振动现象后,天文学家们很快意识到了在恒星上测量类似振动的巨大价值。在长达十年的时间内,人们声称有一些探测结果,但Kjeldsen和Bedding等人认为,此前的结果没有一个是令人信服的。然而,现在已经很清楚,Brown等人发现的F5型星Procyon的功率过剩确实是由类似太阳的振动引起的,这是首次在其他恒星上发现类太阳振动[5]。
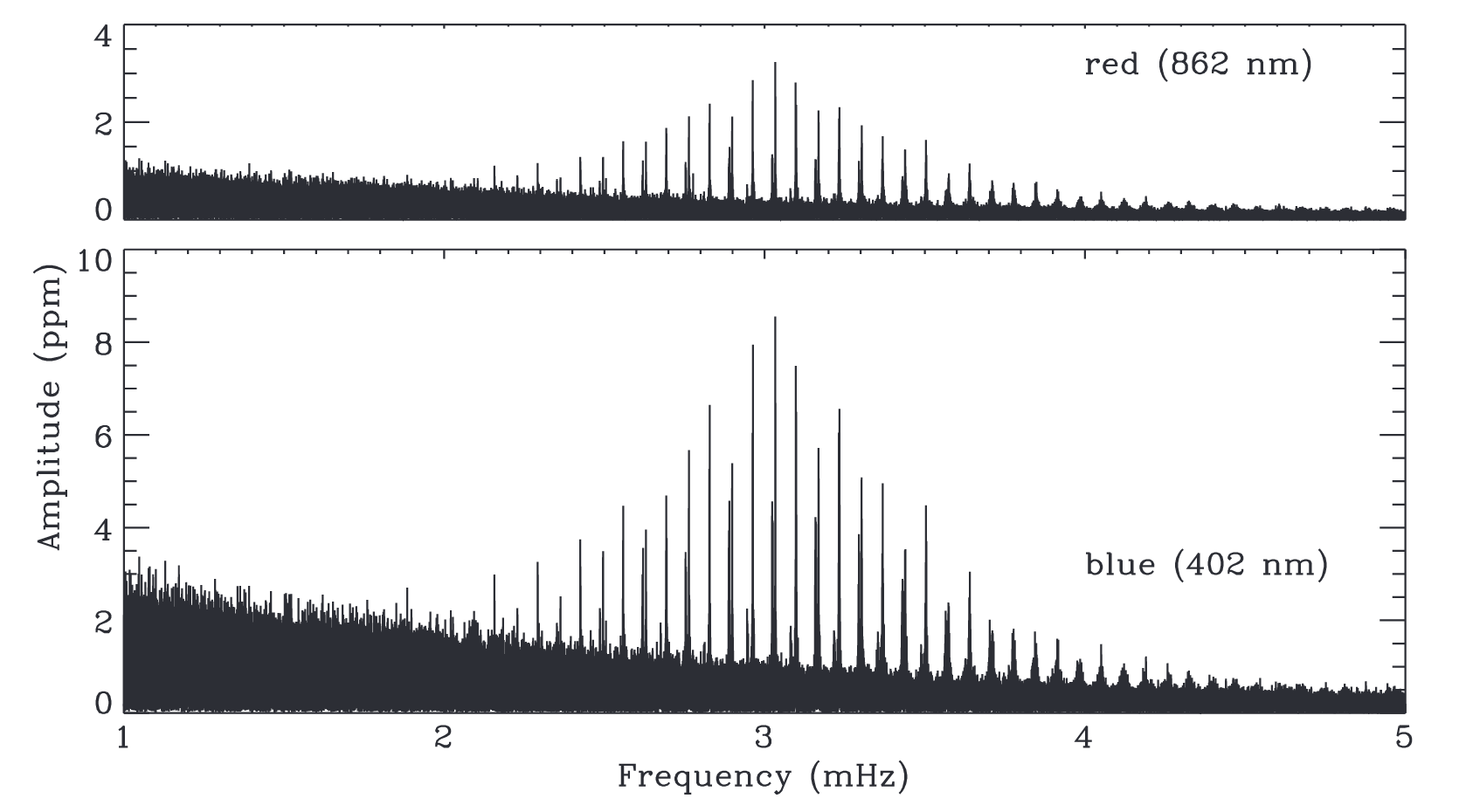
图1. 太阳全局振动的振幅谱
物理图像
基本信息
太阳中的振动是由对流随机激发的,激发的随机性产生了较宽频率范围内的振动,在太阳中约为1至4兆赫兹。对恒星而言,想要产生类太阳振动,它必须足够冷以拥有一个表面对流区。这意味着它的温度应该比经典不稳定性带的红边还要低,这个带包括更晚型的主序星,较冷的亚巨星,甚至红巨星。事实上,现在已经在数千个G型和K型巨星中观测到类似太阳的振动,它们以小时(甚至更长的时间)为周期进行振荡。还有充分的证据表明,半规则变星(M型巨星)的脉动也为类太阳振动[6]。
根据定义,类太阳振动是在恒星外对流区随机激发的,鉴于表面对流被认为会抑制κ机制的作用[7],似乎类太阳振动和κ机制是相互排斥的。但事实上,两者都可以在恒星中存在,前提是表面对流层很薄。有来自Kepler卫星的数据表明,至少有一个δ Scuti star中存在类太阳振动[8]。类太阳振动目前已被用于确定恒星的质量和半径,从而改进对观测行星质量和半径的测量。
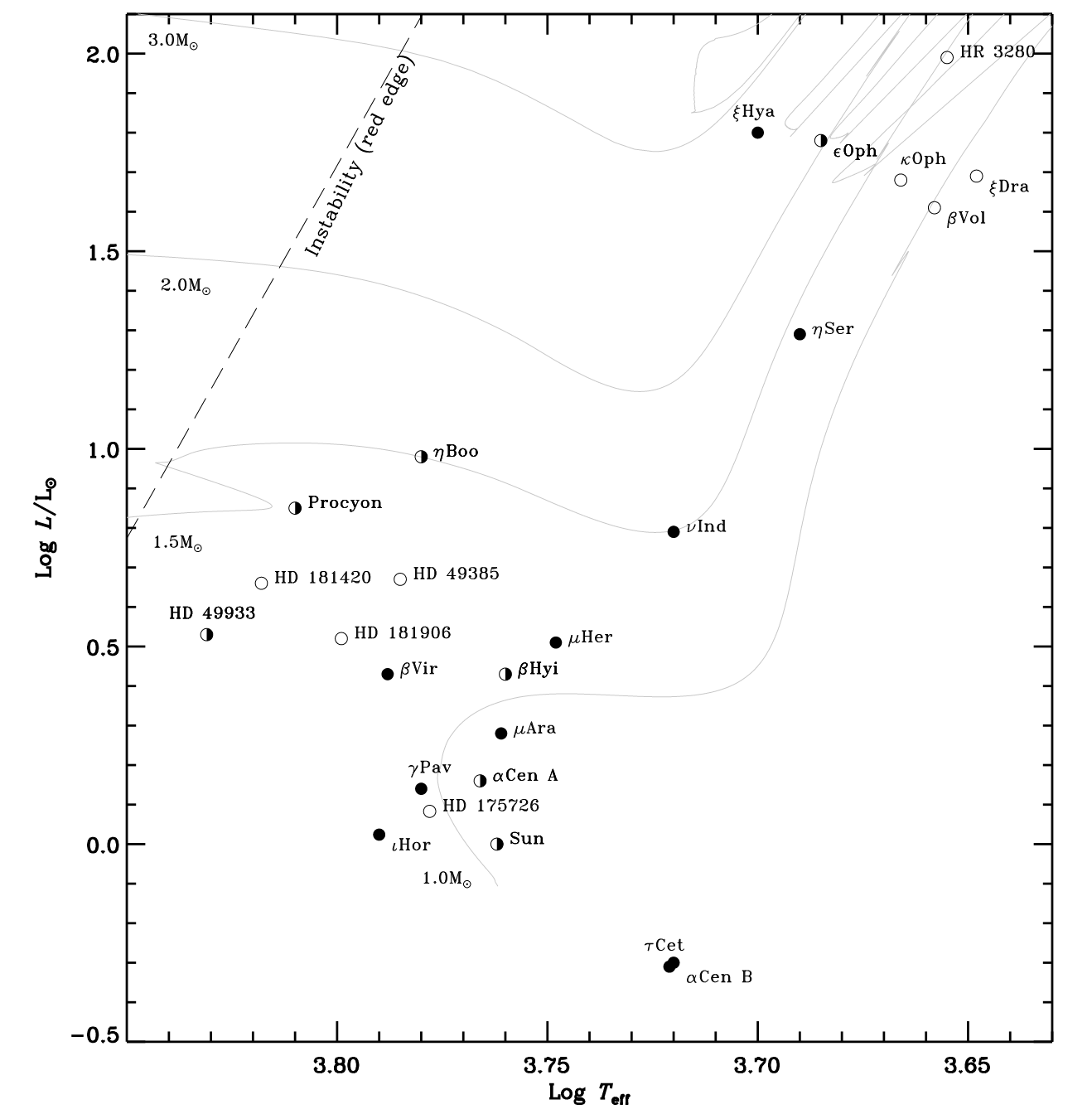
图2. 部分solar-like stars在赫罗图上的图像
脉动机制
类太阳振动本质上是稳定的:它们被随机地驱动并被近表层对流层的强烈湍流内在地阻尼[9]。因此,恒星表现出类太阳振荡的必要条件是近表面对流层的存在[10]。类太阳振动是驻声波,被称为p模式,有三个特征参数:径向阶数n、角度l和方位角m。低阶p模式振荡的频率由渐进关系合理地近似为:
其中反映了恒星密度,反映了恒星核心处的声速,反映了表层声速。
典型天体
天体基本信息
1.南门二(即半人马座α,简写作α Cen)是位于南天的半人马座中的一个三合星系统,由两颗类太阳恒星南门二甲(半人马座α星A)、南门二乙(半人马座α星B)和一颗红矮星比邻星(半人马座α星C)组成。作为一颗与太阳具有相同光谱类型的邻近恒星,α Cen A显然是星震学的良好目标。 Bouchy和Carrier等人清晰地检测到了它的p模式振荡,这是一个重要的突破。
2.南河三(亦作小犬座α,简写为α CMi)是一颗视星等为0.34的恒星,位于小犬座。其为恒星亮度列表中第9亮的恒星,同时也是该星座最亮的恒星。但据现代观测手段,南河三实为由两颗恒星组成的联星系统,其主星为南河三A,一颗白色F5 IV–V型主序星,伴星为南河三B,一颗DQZ型白矮星。
功率谱

图3. α Cen A的功率谱
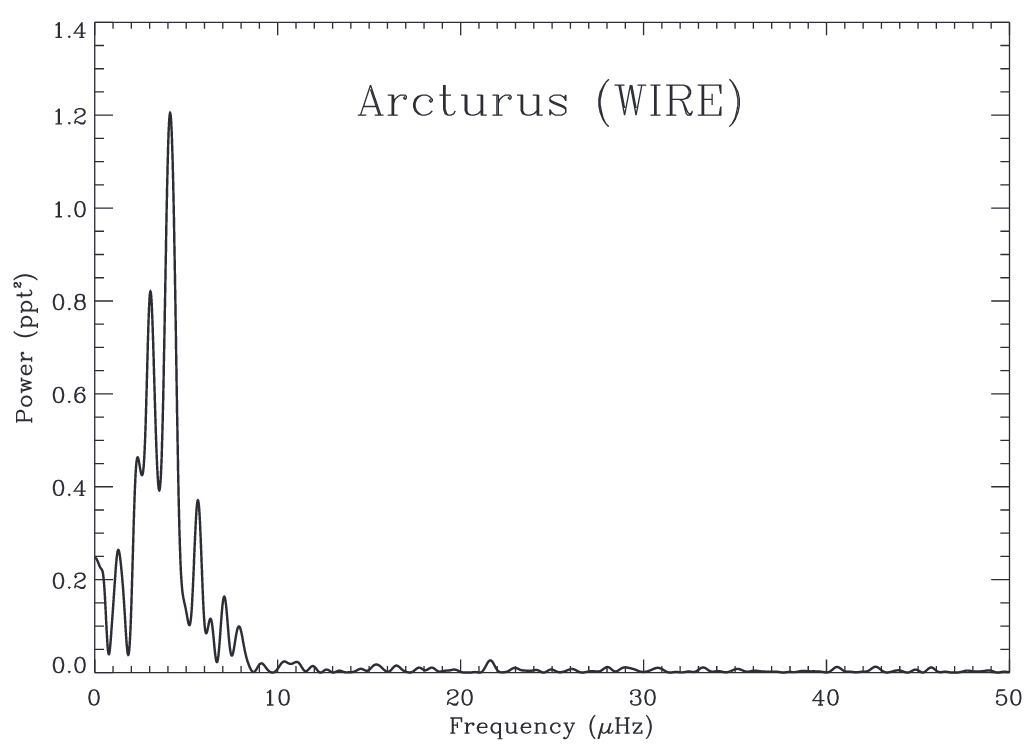
图4. arcturus的功率谱
重要文献
- Bedding T R, Pallé P L, Esteban C. Solar-like oscillations: An observational perspective[J]. by PL Pallé and C. Esteban, 2014: 60.
- Davies G R, Aguirre V S, Bedding T R, et al. Oscillation frequencies for 35 Kepler solar-type planet-hosting stars using Bayesian techniques and machine learning[J]. Monthly Notices of the Royal Astronomical Society, 2015, 456(2): 2183-2195.
- Christensen-Dalsgaard J Ø. Physics of solar-like oscillations[J]. Solar Physics, 2004, 220: 137-168.
- Chaplin W J, Miglio A. Asteroseismology of solar-type and red-giant stars[J]. Annual Review of Astronomy and Astrophysics, 2013, 51: 353-392.
- Bedding T R, Kjeldsen H. Solar-like oscillations[J]. Publications of the Astronomical Society of Australia, 2003, 20(2): 203-212.
参考文献
Noyes R W, Leighton R B. Velocity Fields in the Solar Atmosphere. II. The Oscillatory Field[J]. Astrophysical Journal, vol. 138, p. 631, 1963, 138: 631. ↩︎
Ulrich R K. The five-minute oscillations on the solar surface[M]//Solar Neutrinos. CRC Press, 2018: 390-399. ↩︎
Deubner F L, Mattig W. New observations of the granular intensity fluctuations[J]. Astronomy and Astrophysics, vol. 45, no. 1, Dec. 1975, p. 167-171., 1975, 45: 167-171. ↩︎
Bedding T R. Solar-like oscillations: An observational perspective[J]. Asteroseismology, 2014, 22(404): 60. ↩︎
Martic M, Schmitt J, Lebrun J C, et al. Evidence for global pressure oscillations on Procyon[J]. Astronomy and Astrophysics, v. 351, p. 993-1002 (1999), 1999, 351: 993-1002. ↩︎
Samadi R, Goupil M J. Excitation of stellar p-modes by turbulent convection-I. Theoretical formulation[J]. Astronomy & Astrophysics, 2001, 370(1): 136-146. ↩︎
Morgenthaler A, Petit P, Saar S, et al. Long-term magnetic field monitoring of the Sun-like star ξ Bootis A[J]. Astronomy & Astrophysics, 2012, 540: A138. ↩︎
Uytterhoeven K, Moya A, Grigahcène A, et al. The Kepler characterization of the variability among A-and F-type stars-I. General overview[J]. Astronomy & Astrophysics, 2011, 534: A125. ↩︎
Houdek G, Balmforth N J, Christensen-Dalsgaard J, et al. Amplitudes of stochastically excited oscillations in main-sequence stars[J]. arXiv preprint astro-ph/9909107, 1999. ↩︎
Goldreich P, Murray N, Kumar P. Excitation of solar p-modes[J]. Astrophysical Journal, 1994, 424(1): 466-479. ↩︎